yes 🤖
In a multipolar world they will have credible power projection capabilities.
No. Multipolar means everyone can have multiple independently powerful allies/enemies. It means India, ASEAN, etc. being powerful enough to step in and help ROC when westerners decide to abandon it.
There are a lot of protests in Hong Kong, but the Hong Kong protests was definitely after 2015.
Trade worth considering for Europe. Huh. So fuck the Taiwanese, if that's good for Europe?
This kind of thinking by Westerners is why "multipolar world" as a concept is so popular.
The article over-dramatizes the story. This "deeply wrong" discrepancy is less than 10%. CMB measurements predict a Hubble constant of around 68km/s/Mpc. Distance ladder measurements get around 73km/s/Mpc.
Our current understanding of the universe the Lambda-CDM model is still wildly successful and it's more likely that the true correct model of the universe will be a correction/extension to Lambda-CDM rather than a completely new theory (although if it is a completely new theory that would be pretty cool).
I recommend critically reading the paper. It is quite accessible to those with college-level science background.
Most importantly, it is still highly controversial whether this galaxy rotation direction bias actually exists. If you look at section 4 of the paper, the author is debating against different groups that did similar surveys and found no bias. Someone needs to actually work through this author's methodology as well as those of other groups and figure out what is going on.
If there is indeed a bias, that is super exciting! An anisotropic universe due to being in a black hole would be a very cool explanation. But given the ongoing debate, a general-audience publication like Independent presenting this rotation bias as a given fact is very poor journalism.
Stop depending on these proprietary LLMs. Go to [email protected].
There are open-source LLMs you can run on your own computer if you have a powerful GPU. Models like OLMo and Falcon are made by true non-profits and universities, and they reach GPT-3.5 level of capability.
There are also open-weight models that you can run locally and fine-tune to your liking (although these don’t have open-source training data or code). The best of these (Alibaba’s Qwen, Meta’s llama, Mistral, Deepseek, etc.) match and sometimes exceed GPT 4o capabilities.
Yes, the earth accelerates toward the ball faster than it does toward the feather.
As always, relevant Wikipedia links:
https://en.m.wikipedia.org/wiki/Al-Khwarizmi https://en.m.wikipedia.org/wiki/Donald_Knuth https://en.m.wikipedia.org/wiki/Algorithm
The x axis is position. The y axis is energy. The blue box is a potential energy barrier. The red curve shows the wavefunction of a particle at a certain energy level coming in and tunneling through the wall. (the wavefunction actually live on a different y-scale from this plot and is only superimposed here for illustrative purpose, so don’t use the energy y-scale to read into the amplitude of the oscillatory part).
more info: https://en.m.wikipedia.org/wiki/Quantum_tunnelling
BB84
0 post score0 comment score
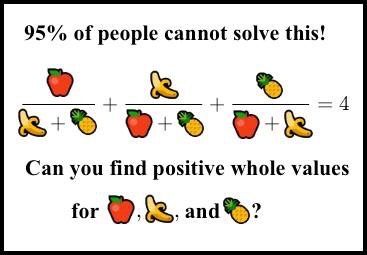

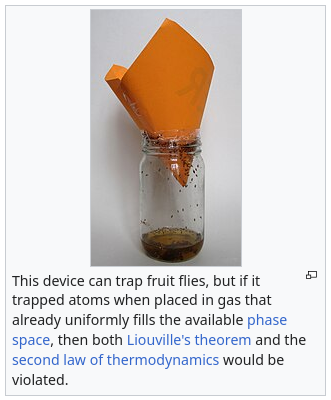






If something is being so heavily subsidized, the correct market response is to buy as much as possible, and resell once the prices ramp up.
Setting up tariffs and complaining about subsidies? 100% not the "free market" response. It's cope.