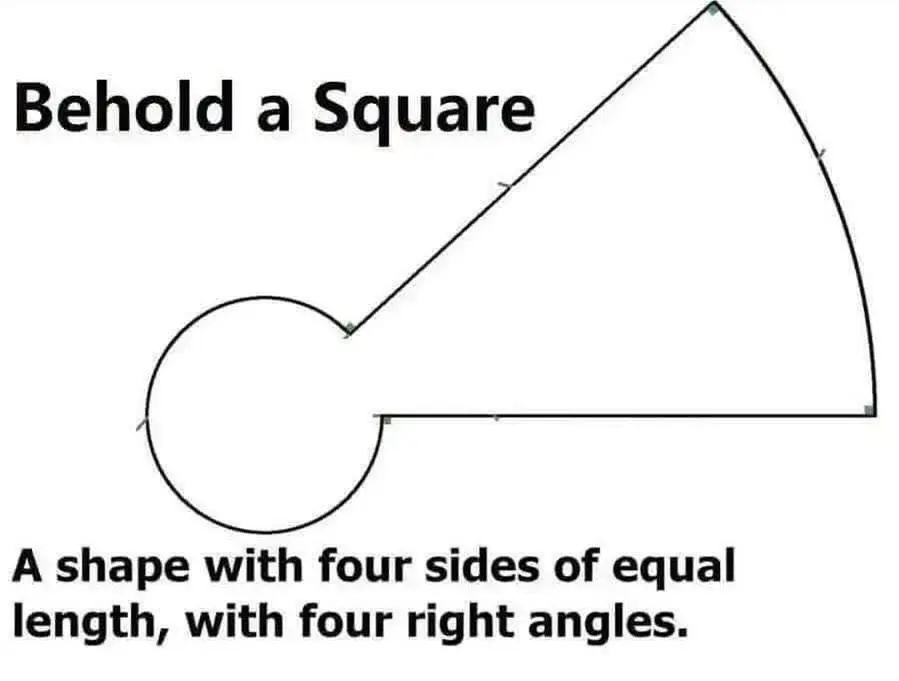
This is why you specify that they are straight, parallel lines.
Perhaps this is just a projection of a square from a non-Euclidean space in which the lines are in fact straight and parallel.
I think the 2D surface of a cone (or double cone) would be an appropriate space, allowing you to construct this shape such that angles and distances around geodesics are conserved in both the space itself and the projected view.
This shape in that space would have four sides of equal length connected by four right angles AND the lines would be geodesics (straight lines) that are parallel.
I suppose you could get a shape like this if you tried to draw a square by true headings and bearings near the North pole of a sphere. "Turn heading 090, travel 10 miles. Turn heading 180, travel 10 miles." and so forth. Start at a spot close to the pole and this will be your ground track.
Actually no it isn't, because attempting to make a square you'd make four turns in the same direction, this would require turning left, right, right, left.
They could be if we're talking about non-euclidian geometry.
The square is a parallelogram, this is not a parallelogram.
I don’t remember all my geometric rules I guess, but can an arc, intersecting a line, ever truly be a right angle? At no possible length of segment along that arc can you draw a line that’s perpendicular to the first.
An infinitely small segment of the arc can be.
Geometrically there isn't a problem. If you draw a line from that point to the center of the arc, it will make it clearer.
I guess if we define it as a calculus problem, I can see the point..
I didn’t mean to pun but there it is and I’m leaving it. Any way, there is no infinitely small section that’s perpendicular. Only the tangent at a single (infinitely small) point along a smooth curve, as we approach from either direction. Maybe that’s still called perpendicular.
A right angle exists between the radius of the circle and the line tangent to the circle at the point that the radial line intersects it. So we can say the radius forms a right angle with the circle at that point because the slope of the curve is equal to that of the tangent line at that point.
Those are not 4 right angles, but 2 right angles and 2 angles of 270 degrees
So 2 right angle and two wrong angle. Got it.
Two wrongs don't make a right, but three lefts will.
but they aren’t parallel
And the right angles are supposed to be inside, not 2 out 2 in
They could be in some n-dimensional spaces
"That's ....like.....just your perspective, man"
You could just use polar coordinates
Going off webster... it looks like this really is only stretching the lines to fit one adjective
A square is a polygon
Yeah, that pretty much sums it up. Wikipedia calls a square a "regular quadrilateral," which seems like a decent enough definition.
Today I learned that when you make up your own inadequate definition, then it's easy to match the definition with something inadequate.
Fuck off, Diogenes!
It wasn't funny when Diogenes did it and it isn't funny now but it keeps getting reposted anyway and we have to pretend it is
I understand Diogenes was usually the life of the party, so they just pretended it was funny.
Philosophers of that era spend a lot of time drunk.
I mean who the fuck dies from laughing to death at a donkey eating figs?
Explain it to a ball
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
This is a science community. We use the Dawkins definition of meme.
