this post was submitted on 08 Oct 2024
1126 points (98.2% liked)
People Twitter
7013 readers
2110 users here now
People tweeting stuff. We allow tweets from anyone.
RULES:
- Mark NSFW content.
- No doxxing people.
- Must be a pic of the tweet or similar. No direct links to the tweet.
- No bullying or international politcs
- Be excellent to each other.
- Provide an archived link to the tweet (or similar) being shown if it's a major figure or a politician.
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
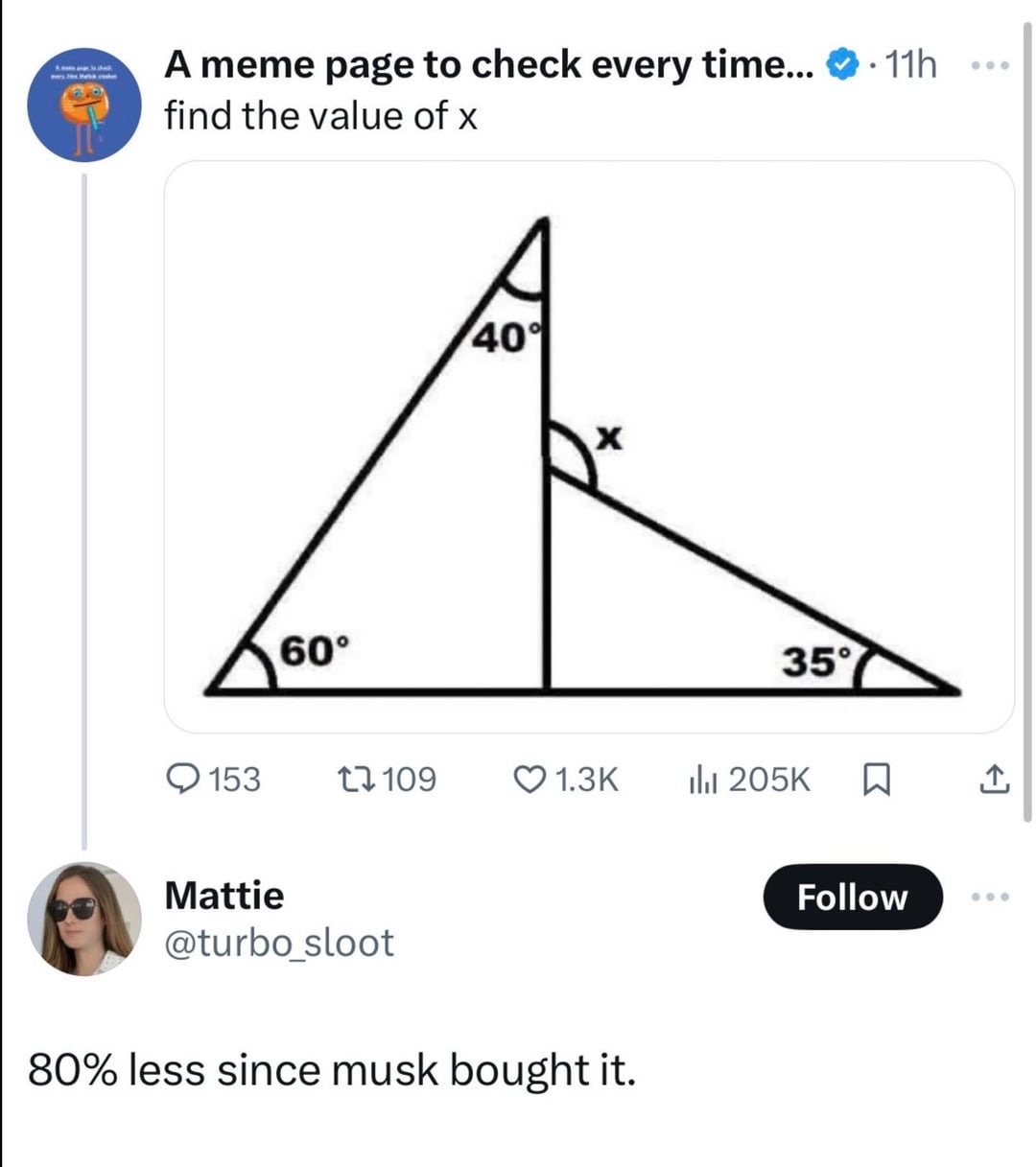
All these people saying its 135 are making big assumptions that I think is incorrect. There’s one triangle (the left one) that has the angles 40, 60, 80. The 80 degrees is calculated based on the other angles. What's very important is the fact that these triangles appear to have a shared 90 degree corner, but that is not the case based on what we just calculated. This means the image is not to scale and we must not make any visual assumptions. So that means we can’t figure out the angles of the right triangle since we only have information of 1 angle (the other can’t be figured out since we can’t assume its actually aligned at the bottom since the graph is now obviously not to scale).
Someone correct me if I'm wrong.
135 is correct. Bottom intersection is 80/100, 180-35-100 = 45 for the top of the second triangle. 180 - 45 = 135
Mathematician here; I second this as a valid answer. (It's what I got as well.)
Random guy who didn't sleep in middle school here: I also got the same answer.
Random woman who didn't sleep very well last night. I got a different answer, then thought about it for 10 more seconds and then got 135.
(No I didn't assume the right angle, my mistake was even dumber. I need a nap.)
You're making the assumption that the straight line consisting of the bottom edge of both triangles is made of supplementary angles. This is not defined due to the nature of the image not being to scale.
Unless there are lines that are not straight in the image (which would make the calculation of x literally impossible), the third angle of the triangle in the left has to be 80°, making the angle to its right to be 100°, making the angle above it to be 45°, making the angle above it to be 135°. This is basic trigonometry.
Yes.
But that doesn't mean that line must be straight. It just means if it isn't, you can't derive x.
Except for the part where it's a single straight line segment, as depicted in the image. Showing the complimentary angles as an unlabeled approximately right angle is within convention. Showing a pair of line segments that do not form a straight line as a straight line is not.
Exactly.
Add to this that
xis literally impossible to calculate if conventions are not assumed, and absolutely possible to calculate if conventions are followed. Assuming the conventions won't hold is an irrational position.What you say makes no sense.
The problem is LITERALLY unsolvable if we can't assume that all the lines are straight.
The schematic was OF COURSE purposefully drawn in a way to make the viewer assume that the third angle of the left triangle is 90°, making the angle to it's right also be 90°, but the point of the exercise is to get the student to use ALL the given information instead of presuming right angles.
And NO, assuming all the lines are straight is NOT unreasonable, it is the only way that the problem could ever possibly have a solution.
I'd say that the shape on the left has what appears to be a little kink right near X, so one might infer that the shape on the left might be a quadrilateral. There are blatantly obvious vertices that are not labeled as such, so we can't assume that the not-quite-straight line is supposed to be straight since other angles are also not explicitly indicated as vertices...
Reasonable assumptions are a fundamental requirement for communication. It's not that you are wrong in what you are saying. There is a chance that the poser of the question made a visual representation of the triangle's sides appear to be complementary and appear to construct a straight line across their bases while not actually definitively indicating them as such.
The way these triangle's are represented is already skewed so perhaps that is what they are trying to do.
The thing is though, at that point they are defying convention and reasonable assumptions so much that they aren't worth engaging seriously because it's flawed communication.
The version people are choosing to answer seriously is equivalent to a guy holding up a sign that says "ask me about my wiener to get one in a flash for free!" while standing next to a hot dog stand. If you ask he flashes his junk at you and says cheekily "haha you just assumed wrong! Idiot!"
That's already dumb enough but some people could see the clues that suggest he was actually intended to flash people the whole time through a series of reasonable assumptions about his outfit lacking pants or the hit dog stand not even being turned on.
Your argument that we can't assume the line at the bottom is straight is like saying we can't assume the theoretical trenchcoat man won't toss a rabid dachshund he was hiding under the coat at us because the hot dog stand has no buns or condiments on it.
You might not be provably wrong but it's really not worth thinking like an insane person just because a few conventions were defied
So why do you assume the diagram depicts Euclidian space? Why do you assume the numbers are base 10? Why do you assume the question is in English, not just some language that looks like English but has different semantics?
Following your logic, there is no evidence that these are triangles and it is never stated, therefore none of these lines might be straight and the discussion is irrelevant.
There is also no evidence that these are lines at all and not just unconnected points that are offset on a subpixel scale. Or indeed there is no evidence that they are using base 10 numbers or aren't asking a completely different question in an invented language that just happens to look like English but has totally different semantics.
The people claiming it is unsolvable because one 110/80 degree pair of angles looks like a 90/90 one are ridiculous.
When you're finding the outside angle along the line of a triangle you don't need the inside angle tied to that outside angle if you have the other two inside angles since both straight lines and triangles total to 180 degrees.
This is a standard way to draw geometric proofs, it's not at all unreasonable to assume straight lines alongside unrepresentative angles. It's certainly still an assumption, but a conventional one.
I mean, the assumption shouldn't be anything about scale. It should be that we're looking at straight lines. And if we can't assume that, then what are we even doing.
But, assuming straight lines, given straight lines you find the other side of an intersecting line because of complements.
That's exactly what the other user is saying. We can't assume straight lines because the given angles don't make any sense and thus this graph is literally impossible to make. We're arguing over literal click bait is what we're doing.
Why do the labeled angles prevent us from assuming straight lines?
Because the angles aren't represented accurately. It could be that the two angles that look like they're 90° add up to 180°, but they could also not
That's technically possible, but that's also an irrational take. The rational take is to assume the problem is solvable given the available information, which means assuming that the lines are straight.
Yes, two angles appear to be 90⁰, but they're obviously not with the given information. Math conventions nearly always label right angles, so not having the right angle there implies that the angle should not be assumed to be 90⁰. Math conventions in trigonometry also generally assume straight lines unless there's a visual indicator that they're not, and those tend to be exaggerated so it's obvious.
So the rational answer here is that the bottom line is straight and therefore the problem is solvable. Saying otherwise is irrational, because that's so far away from math conventions.
Because the apparently straight lines contradict the labels. As drawn, the unlabeled bottom vertices are clearly 90°, not 80° and 100°. We must either conclude that the labels are incorrect, or that the figure is not drawn to scale. Either way, it's insoluble.
We can't assume that the straight line across the bottom is a straight line because the angles in the drawing are not to scale. Who's to say that the "right angle" of the right side triangle isn't 144°?
If the scale is not consistent with euclidian planar geometry, one could argue that the scale is consistent within itself, thus the right triangle's "right angle" might also be 80°, which is not a supplement to the known 80° angle.
thx for the compliment
I'd argue that the bottom line is indeed one continuous line regardless of how many other lines intersect on it, because there's nothing indicating that the line is broken at the intersection.
Now the only reason I think the lines are straight at all is use of the angular notations at the ends, which would be horribly misleading to put at the end of curves or broken lines.
Stupid stuff like this is why kids hate math class. Unless the problem says calculate all unmarked angles, those visually 90 degree angles are 90 degrees. It works that way in any non engineering job that uses angles because it's common sense.
...what? I get that this drawing is very dysfunctional, but are you going to argue that a triangle within a plane can have a sum of angles of 190°?
Nope I'm not saying that. I'm saying this is a gotcha question that demotivates learners.
I see. I agree completely. The only place this belongs is as a thought experiment on making assumptions in geometry.
The sum of the angles of a triangle are always 180°
Yes, I believe I implied this by suggesting that the sum of angles being 190° is absurd.
No, they're saying that unless you're already good at this stuff, it's easy to assume that a visually 90° angle is actually 90° even when it's not
Especially if you are bad at this stuff you know that drawing anything like that accurately is a real pain and nobody who can avoid it will ever do it to represent anything accurately. That is what labels are for.
You're making the assumption that they are triangles.
Your assumption is that it's a Cartesian coordinate system with 90° angles. But that's not necessarily the case. You can apply a sheer transformation to correct for the unusual appearance. When you do that, the angles change, but straight lines stay straight and parallels stay parallel. There's a mathematical term for that, which I can't remember right now.