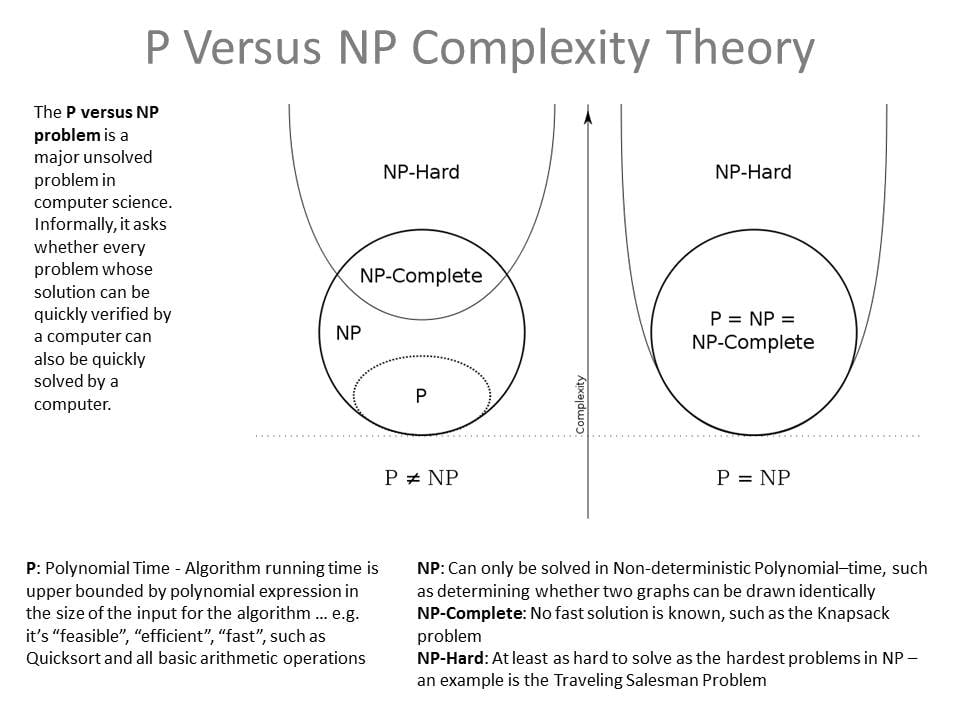
They are classes that describe how hard a problem is.
Imagine trying to explain to someone how fast you can do something, for example sorting a list. The simplest way would be saying "I can do that in two seconds" but that's not very helpful because it depends on how fast your computer is. A better way would be to express it as a number of steps: "I can do that in 10000 steps". For this ELI5 explanation the exact definition of what a step is doesn't matter that much, it could be a single CPU instruction or a comparison between two items in the list.
That gets you a bit closer but obviously, how complex sorting a list is, depends on the list: how long is it and how scrambled is it? Short lists are faster to sort than long ones and lists that are already (almost) sorted are usually fasterto sort than ones in reverse or completely random order. For that you can say "In the worst case, I can sort a list in three times the number of items squared, no matter the initial order". When writing that down, we call the number of items n, so the total work is 3 * n^2. The bigger n gets, the less the constant factor matters, so we can leave it out and instead write O(n^2). This is, what people call "Big O notation" and it's the reason why I said the exact definition of a step doesn't matter that much. As long as you don't get it too wrong, different step definitions just change the constant that we're ignoring anyway. Oh and by the way, O(n^2) for sorting lists isn't that great, good algorithms can reach O(n*log(n)) but I didn't want to throw logarithms at you right away.
Now we get close to understanding what P is. It's the class of all problems that can be solved in "polynomial" time, so O(n^a) for any number a. Note that only the highest exponent is relevant. With some work we could prove that for example O(n^3 + n^2 + n) is equivalent to O(n^3). Examples of problems in P are sorting, route planning and finding out if a number is prime.
I'm running out of time because I have some errands to run, maybe someone else can explain NP (nondeterministic polynomial time). If not, I'll add a follow up later today.