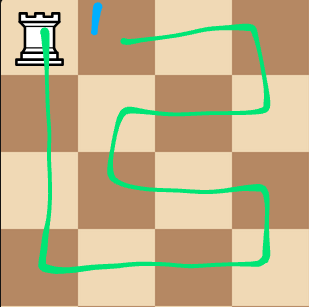
Any route from white to white visiting N white squares must visit exactly N-1 black squares. Any route from white to black visiting N white squares must visit exactly N black squares. Therefore on a board with an equal amount of white and black squares, it's not possible to walk a route from a white square to a white square and visit all squares.

You can prove it through induction. Starting with a route that visits just one white square, you visit zero black squares. Then, if you want to extend your route with one white square, you must also visit exactly one black square to get to it, as no two white squares border one another. Meaning for a route of S steps (where each 'step' is actually two moves from a white square to the next white square), you visit S+1 white squares and S black squares, or equivalently N white squares and N-1 black squares.

All the grids have even number of squares (equal black and white). Therefore it is impossible to start on white and end on white while covering everything else.

I don't have the formal proof for this, but can be proven with examples. In each of your grids.

I'll be following this thread to see if someone shares the formal proof for this, fingers crossed!

This puzzle is definitely impossible. In fact it seems to be some sort of parity issue, although I'm having trouble with the actual proof. Basically if you always keep the start in the top left corner, then you can only complete a rook's tour if the end square has an odd manhattan distance (x distance + y distance). If you put the end square an even manhattan distance away, then you create this issue where you're always unable to hit one square.

For example, even parity, impossible:

Odd parity, possible:

doesn't visit usually mean "ends movement in that square"? 'Cause that means skipping squares is allowed. So just fill out the board until the last row and skip ahead of the end tile while doing so. Do the last row in an order that the last col is the same col as the end square, move to end square.

Uhhhh yeah?

I found this to be really easy but I don't play chess so maybe I'm misunderstanding or perhaps the question was worded wrong?

Using these rules from your post

"Starting from a8, could a rook visit every square on the board once, ending on f3?"

And standard rook movement

I came up with this solution.

Follow the numbers up or down from the start or finish. Highlighted squares show moves to squares that aren't adjacent.

I'd imagine there's lots of solutions with different patterns, this is just the one that came to me on the fly.

… unless I don’t fully understand the problem.

You're forgetting knook promotion when you reach the opposite side, combining the knight and rook tour, making it possible again