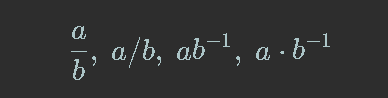Starting a new comment thread (I gave up on reading all of them). I'm a high school Maths teacher/tutor. You can read my Mastodon thread about it at Order of operations thread index (I'm giving you the link to the thread index so you can just jump around whichever parts you want to read without having to read the whole thing). Includes Maths textbooks, historical references, proofs, memes, the works.
And for all the people quoting university people, this topic (order of operations) is not taught at university - it is taught in high school. Why would you listen to someone who doesn't teach the topic? (have you not wondered why they never quote Maths textbooks?)
#DontForgetDistribution #MathsIsNeverAmbiguous